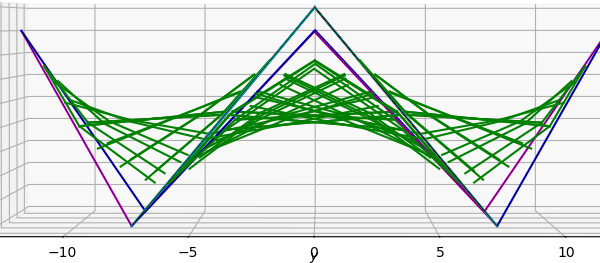
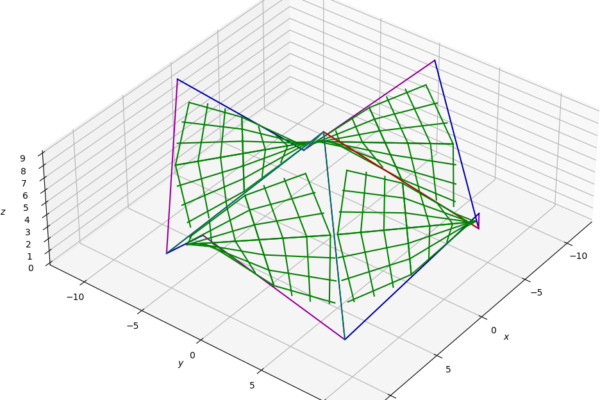
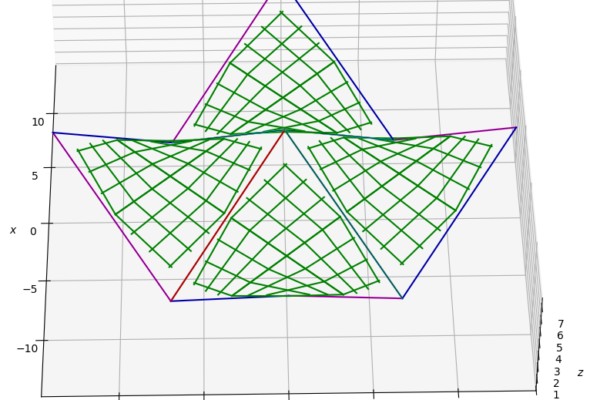
Hyperbolische Paraboloide

Hyperbolische Paraboloide sind Sattelflächen, die entstehen, wenn man zwei gegenüberliegende Kanten gleichmässig durch Fäden verbindet. Diese geometrisch höchst spannenden Figuren sind unter Architekten wohlbekannt, und auch die Jugendverbände realisieren häufig Sattelflächen mittels dünnen Seilen. «Das geht auch mit Blachen!», dachten wir uns, und begannen eine mathematische Reise durch Regelflächen, negative Gauss’sche Krümmungen, Konoide und Quadriken.

Die Entwicklung eines Zeltes beginnt bei uns immer mit einem geometrischen Modell. Abwickelbare (einfach gekrümmte) Flächen lassen sich als Papierbogenmodell einfach und effizient konstruieren; anders sieht die Situation bei nicht abwickelbaren (doppelt gekrümmten) Flächen aus. Bei diesen Figuren führt kein Weg an einem massstabsgetreuen Stoffmodell oder einer exakten mathematischen Betrachtung vorbei. Da wir oft mehrere Zeltgrössen ausprobieren, fahren wir häufig doppelspurig: Ein parametrisiertes mathematisches Modell, das die Zeltgeometrie sauber rechnet und schnell verschiedene Varianten erkunden lässt, und ein massstabsgetreues Stoffmodell zur Validierung der Geometrie und zur Simulation des Aufbaus.

HP in Python

Das mathematische Modell programmierten wir in Python, und als frei wählbare Parameter konnten die jeweiligen Anfangs- und Endpunkte der Träger und die Anzahl Blachen und Flächen gewählt werden. Spannend war da die Fragestellung, ob genügend Platz bleibt, um die Mittelblachen auf den Träger spannen zu können, welche Trägerwinkel ästhetisch erscheinen und statisch noch vernünftig sind, und wie gross der Zentriwinkel einer Sattelfläche sein soll.

Stoffmodell

Als wir zufrieden waren mit einem Parameterset, bauten wir ein Stoffmodell im Massstab 1:50 einer Variante mit 9m Trägerhöhe in der Mitte, 7.5m Aussenträgerhöhe, Kantenlänge 6 Blachen sowie 4 Flächen auf. Durch die leichte Dehnbarkeit des Stoffes ergab sich ein geometrisch perfektes Modell, wobei wir entdeckten, dass symmetrische Höhen nochmals ein deutlich ansprechenderes Design ergeben. Das Modell brachte auch Tücken zum Vorschein: Wie verbinden wir 4 Rundhölzer auf einer Höhe von 9m miteinander? Wie lassen wir die Rundhölzer im Erdreich perfekt zusammenlaufen? Und wie befestigen wir die Blachen an dem Träger, respektive wie lenken wird die Seile um, ohne zu viel Distanz zu verlieren?

Aus 4 mach 9

Unerwartet konnten für den Erstaufbau unseres Pringles-Zeltes keine langen Rundhölzer organisiert werden, sodass wir uns notgedrungen dafür entschieden, Flächen mit lediglich 9 anstelle der 36 Blachen zu bauen. Als Trost erhöhten wir die Anzahl Sattelflächen von 4 auf 9, und griffen bei der Realisierung in die Trickkiste: Gerade Träger kann man auch mit Zurrgurten (Spannsets) realisieren, anstelle von Hölzern, was den Bau massiv vereinfacht hat. Um saubere Umlenkpunkte zu haben, fädelten wir Stahlringe auf die Spannset auf, deren Position wir mit Zurrfix (Spanngurten) sauber einstellen konnten. Der obere Anschlagpunkt für die Spannset war ein 3.25to-Schäkel, den wir in eine M20-Gewindestange einfädelten und so mit den Holzträgern verbanden. Das ermöglichte uns, komplett auf Rundschlingen zu verzichten, wodurch sich ein sehr sauberer und äusserst ästhetischer Bau ergab. Perfekt, um in Turtmann anfangs September Schattenflächen für alle Teilnehmenden des Jumbo (Grossanlass Jubla Wallis) zu bieten!